Notes on Dynamo (2007)
Sat Mar 20 2021tags: programming computer science self study notes public 6.824 MIT distributed systems
Introduction
I read the following the paper as part of my self-study of 6.824 with NUS SoC folks. It may or may not be part of my goal to finish a Stanford CS degree in a year.
This week we discussed the paper [DeCandia et al. (2007). Dynamo: Amazon's Highly Available Key-value Store](https://files.lieu.gg/docs/DeCandia et al. (2007). Dynamo--Amazon's Highly Available Key-Value Store.pdf)
Some useful links are the 6.824 lecture notes and the 6.824 lecture FAQ
The big picture
Dynamo is trying to build a distributed key-value store focusing on write availability and write latency.
Motivation: Amazon doesn't need a RDBMS for many of its services, only a key-value store: "There are many services on Amazon's platform that only need primary-key access to a data store... for many services... the common pattern of using a relational database would lead to inefficiencies and limit scale and availability."
So we have a more relaxed operations model: we only require getting and setting keys. However, there are two things we care about a lot:
Firstly, Amazon cares a lot about latency, because any weak link in the chain will result in cascading latencies on the rest of the services.
Secondly, we want it to be always writeable
despite failures.
In traditional systems, "writes may be rejected
if the data store cannot reach a majority of the replicas
at a given time." This is unacceptable to Amazon:
e.g. you can't have Amazon reject adding items to shopping carts.
Here Amazon allows you to tweak the parameters:
if you always want writes to succeed,
you can set W to 1, which ensures that a write
is accepted as long as a single node in the system
has durably written the key to its local store.
"However, in practice, most Amazon services in production
set a higher W to meet the desired level of durability."
Also, we don't care about consistency so much: "data stores that provide ACID guarantees tend to have poor availability." Instead DynamoDB guarantees eventual consistency.
Big ideas
Consistent hashing allows incremental scalability
Dynamo uses consistent hashing, which allows nodes to be added and removed on-demand very quickly. Let's see how it does this.
Why do we need to hash?
Before talking about consistent hashing, let's talk about hashing. Why hash? We hash in order to allocate keys evenly to nodes. Each node is responsible for only a small set of keys (called its range), because the number of keys is too large for any single node to hold.
When a node receives a read or write request for a key, it will hash it, then check if that hash is in its range. If it is then it will service that request. If it receives a request for a key not in its range, it will forward the request to the correct node. (How does it know who to forward the request to? More on this later.)
What is consistent hashing and how does it allow for incremental scalability?
OK, so that's hashing. What about consistent hashing? The idea of consistent hashing is to simply wrap the range around, so the largest value wraps around to the smallest value. Wikipedia says that consistent hashing is a special kind of hashing such that when a hash table is resized, only a few keys need to be remapped on average.
Why is this necessary? We'll soon see that consistent hashing allows incremental scaling in the sense that adding a new node only changes the keys of N nodes (where N is small -- 3), while using non-consistent hashing would require all keys to be remapped on average.
How do we use consistent hashing?
So in consistent hashing the key space is mapped to a big circle where the largest hash value (in this case, ) wraps back to zero.
Note that consistent hashing is a different thing from replicating the data on multiple nodes. Consistent hashing allows for replication and scalability, but you can use consistent hashing without replication.
How are nodes assigned to keys
Each node is randomly assigned a point on the consistent hashing circle, and it's responsible for all points between it and the previous node on the circle.
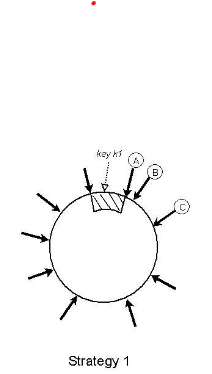
The above figure illustrates. Here the key k1 lies between the node to its left (not labeled) and the node to its right (A). So A is responsible for key k1.
How does consistent hashing allow scalability?
Recall that nodes are assigned to a key range using random assignment. What happens when we have to add or remove a node? If we remove a node then we must make sure that that node's key range is somehow given to the remaining nodes. And conversely if we add a node then we must "steal" some keys from all the nodes to give to the new node. Consistent hashing allows us to do this affecting the minimum amount of nodes.
Let's compare what happens when we add a node under
consistent hashing versus non-consistent hashing.
Suppose you had a 3-bit hash function hash(key) that mapped keys
uniformly to an integer in range[0, 7] inclusive.
And suppose that you had three nodes so each hash(key) mod 3
would give a key of 0, 1 or 2.
Let's look at how each of the keys maps in mod3:
0 : 0
1 : 1
2 : 2
3 : 0
4 : 1
5 : 2
6 : 0
7 : 1
Now suppose a new node enters the cluster The key insight is that almost all of the hashes have changed (I've marked the keys that have changed with asterisks):
0 : 0
1 : 1
2 : 2
3 : **3**
4 : **0**
5 : **1**
6 : **2**
7 : **3**
This will mean that a vast majority of data (those which mapped to 3--8) has to be moved from one cluster to another. In fact, if N is small and the domain of the hash function, K, is large such that , almost all of the data will have to be moved. The same is true if we remove a node from the cluster.
Consistent hashing avoids this problem. In the basic version of consistent hashing each hash is assigned to a node with the first ID larger than it, and each node is randomly assigned a key value. Again we'll use the three-bit hash function with three machines. Here's a very badly-drawn circle with the three nodes denoted with asterisks. In this case the three nodes have been assigned 0, 2 and 5 respectively.
*0
7 1
6 *2
*5 3
4
0 : 2
1 : 2
2 : 5
3 : 5
4 : 5
5 : 0
6 : 0
7 : 0
Now let's insert a new node with value (say) 4:
*0
7 1
6 *2
*5 3
*4
0 : 2
1 : 2
2 : **4**
3 : **4**
4 : 5
5 : 0
6 : 0
7 : 0
As we can see, only the nodes in between 2 and 5 need to be moved.
In general, using consistent hashing means that adding or removing a new node only requires minimal inter-node communication/key range changes, which allows for scalability.
How does consistent hashing allow replication?
In order to ensure durability/availability,
you can't have only one node save the data.
The data must be replicated over multiple nodes:
N nodes, to be exact.
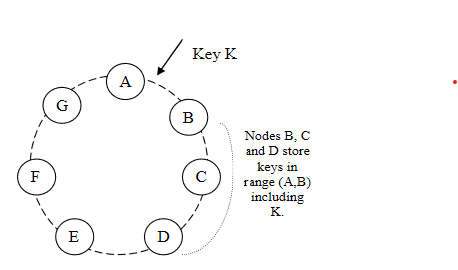
Figure 2 illustrates how this is done.
The N-1 nodes clockwise of the key range
replicate the keys of that node.
The keys that fall within (A, B]
are the purview of B.
The two other nodes C and D that lie clockwise
of B will replicate this key range too.
There's the idea of a preference list: a preference list is the list of physical nodes responsible for storing a particular key. (We'll see why I mention the word physical later.)
Having virtual nodes (tokens) improves on consistent hashing
Section 4.2 of the Dynamo paper:
The basic consistent hashing algorithm presents some challenges. First, the random position assignment of each node on the ring leads to non-uniform data and load distribution. Second, the basic algorithm is oblivious to the hetereogeneity in the performance of nodes. To address this issues... instead of mapping a node to a single point in the circle, each node gets assigned to multiple points in the ring... Dynamo uses the concept of "virtual nodes". A virtual node looks like a single node in the system, but each node can be responsible for more than one virtual node.
Why is this an improvement? The MIT Aurora FAQ says:
They are a scheme to balance the keys nicely across all nodes. If you throw N balls in B bins, you get on average B/N balls in a bin but some bins may have many balls. To ensure that all bins are close to the average, you can place multiple virtual bins in each real bin. The average of multiple random variables has lower variance than a single random variable.
How does one assign nodes to keys?
Amazon actually iterated over three versions of assigning nodes to keys.
Vector clocks and hinted handoff allows for an always-writable database
The next big idea is to allow reads to return not just a value, but a tree of possibly-inconsistent values. This is in effect giving up the consistency property of "reads must observe the latest write": now reads may observe lots of different writes, one of which is the latest. If you allow this then you can make your database always writeable, which is Amazon's explicit design goal. We'll also see how nodes make sense of the different writes.
So what exactly happens in a read/write?
Read and write operations involve the first N
healthy nodes in the preference list,
skipping over those that are down or inaccessible.
Whenever a node receives a read or write request on an object,
it will increment its own sequence number.
For a get() request, the coordinator
requests all existing versions of data for that key
from the N highest-ranked reachable nodes,
then waits for R responses before returning the result
to the client.
If the coordinator ends up gathering multiple versions
of the data, it returns all the versions it deems to be
causally unrelated.
The divergent versions are then reconciled and
the reconciled version superseding the current versions
is written back.
Note that with eventual consistency,
it's not guaranteed that the data it gets back
reflects all the writes!
For a put() request, the coordinator generates
the vector clock for the new version
and writes the new version locally.
In Dynamo, all objects are immutable,
so the only way to change an object is to generate
a new version.
It then sends the new version (along with the new vector clock)
to the N highest ranked reachable notes.
If at least W-1 nodes respond then the write is considered
successful.
How vector clocks are used in reads/writes
So what's a vector clock?
A vector clock is effectively a list of (node, counter)
pairs. List[Tuple[Node, Counter]]
One vector clock is associated with every version of every object.
(Objects are immutable).
One can determine whether two versions of an object are on parallel branches or have a causal ordering by examining their vector clocks.
How do we use vector clocks to determine if two versions of an object are causally ordered or are diverging branches? "If the counters on the first object's clock are less-than-or-equal to all of the nodes in the second clock, then the first is an ancestor of the second and can be forgotten. Otherwise, the two changes are considered to be in conflict and require reconciliation."
Handling failures
Hinted handoff
Dynamo allows writes to return to the caller
before the update has been applied at all the replicas:
"Upon receiving a put() request for a key,
the coordinator generates the vector clock for the new version
and writes the new version locally. The coordinator
then sends the new version (along with the new vector clock)
to the N highest-ranked reachable nodes.
If at least nodes respond
then the write is considered successful."
Note the word reachable here. This is what hinted handoff is: some less-preferred nodes will help keep some data meant for the preferred, unreachable node. and try to periodically re-deliver it to the preferred node which is temporarily down. Once the transfer succeeds the less-preferred node will delete the object from its local store. This is used for temporary node failures.
This gives us the eventual consistency property any read request will eventually read all of the values that were written because the less-preferred nodes will deliver it to the preferred nodes as long as fewer than W nodes fail.
But note that hinted handoff loses consistency. See the FAQ for this: in particular, "Why is Dynamo only eventually consistent?"
Replica synchronisation
Basically Dynamo compares nodes using Merkle trees,
which allows log(N) comparisons in the average case.
Membership and failure detection
Used for permanent node failures. An administrator manually adds and removes. Not that interesting IMO.
How this relates to other database designs
Dynamo vs Aurora
The biggest difference is that Aurora is a RDBMS, Dynamo is a key-value store. Although it seems to me that Aurora could easily be made into a kv-store as well; since "the log is the database", just restrict the set of transactions to be only get and put.
In Dynamo every node is capable of receiving a write, while in Aurora there's only a single write-capable replica. This may have scalability implications, since Aurora is fundamentally limited to one writer.
In Aurora each storage segment stores 10GB segments of the log; here each node stores a partition of the entire key space. Aurora supports a storage volume up to 64TB; this is pretty big, but Dynamo can do even bigger. Since each node has its own storage, the storage limit its limited only to the key space. The key space is 128-bit. 232 is 4GB, 264 is 18.4 exabytes, and 2**128 is a ridiculous number.
Dynamo vs Memcached
Memcached and Dynamo are both key-value stores. But they solve very different problems. Memcached is trying to make reads very fast: Dynamo is trying to make writes very fast (and always available).
Memcached's writes are going to be very slow because the writes have to propagate to all the regions (? is that true?).
Again there may be differences in storage: for memcached there must be a single database instance and that probably bounds the number of keys you can have, whereas for Dynamo you could have loads of keys since each node only holds a small subset of keys.
FAQ
What are the three different partitioning strategies and why is the third one best?
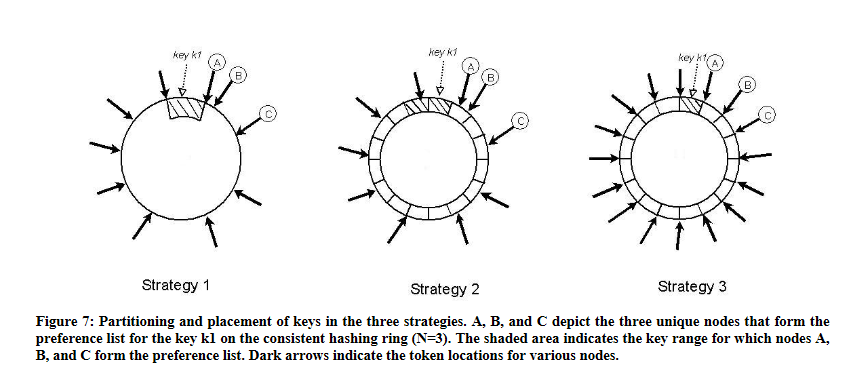
This is the trickiest part of the paper, IMO. So here we're talking about how to assign nodes (both real and virtual) onto the hash space. And there are three approaches.
The first version and the one that's explained in section 4.2 is that each node is assigned several virtual nodes (tokens) and each token is randomly placed on the entire hash space. Each token is responsible for the keys between it and the token anticlockwise of it. We call this a key range.
But there's a problem with this. Section 4.7, Replica synchronisation:
The disadvantage with this scheme is that many key ranges change when a node joins or leaves the system thereby requiring the tree(s) to be recalculated. This issue is addressed, however, by the refined partitioning scheme described in Section 6.2.
Let's explain this a little bit more. Let's take a look at Strategy 1 in the diagram. Let's call the node to the left of A node O. When say node A is removed, the new key range will stretch from O to B. And that means that node C has to change its key range, looking up all the new keys individually and grabbing the keys and so on. This takes a long time. As the paper writes, the fundamental issue is that adding and removing nodes changes the data partitioning. So let's try to decouple these things.
The second approach is a middle-of-the road approach. You place the tokens exactly where you would in the first version, (random assignment). But the difference is in how you assign keys to tokens. Here the key ranges never change: instead, the key space is divided into equal-size partitions and these partitions are then assigned to tokens. A key is assigned to a token by walking from the end of its partition. This approach is better because when a node leaves or is added the key ranges don't change, so you can actually copy and move over partitions wholesale from one node to another. Also, you can simply add more nodes without changing the key range, thus decoupling the partitioning from the number of nodes.
The third approach is actually really simple.
Again you divide the key space into equal-size partitions,
but the difference here is that instead of placing tokens
randomly along the ring, here you place tokens
uniformly (but not randomly!) along the ring.
In fact, you assign Q/S tokens to each node,
where is the number of nodes.
And when nodes are added or removed you simply
randomly distribute tokens to or from the nodes
such that each node maintains tokens.
So instead of transferring key ranges from node to node,
you simply transfer token ownership from node to node
(which of course transfers the attendant tokens as well).
What are the parameters R, W, and N? Assuming there's no "hinted handoff", how many node failures can the system tolerate while still ensuring that successful read operations return up-to-date data?
N is the number of nodes any data item is replicated to. "In addition to locally storing each key within its range, the coordinator replicates these keys at the N-1 clockwise successor nodes in the ring. This results in a system where each node is responsible for the region of the ring between it and its Nth predecessor".
R is the minimum number of nodes that must participate in a successful read operation.
W is the number of nodes that must participate in a successful write operation.
"hinted handoff": a node stores some data that isn't meant for it, but keeps a record who it's meant to be for, and will deliver the replica to the intended recipient once the recipient has recovered.
Suppose we are looking at the following sequence of events:
- get() call
- put() call
- get() call <--- successful, but must return up-to-date data.
I think the answer to the question depends on when the nodes fail. If the nodes fail after the successful put call, then as little as nodes need to fail (where ) in order for subsequent successful get() calls to no longer be up-to-date. In the worst-case scenario, all W nodes that held the latest version of the object written to have failed, and you lose your updated data (until you can bring it up again).
Call this the durability condition.
If however the nodes fail before the put call (or even before the first get call), the maximum number of node failures the system can tolerate is
Call this the availability condition.
Why is this? Suppose there is no hinted handoff and we have consistent data replicated over N nodes. In order to perform a successful read there must be at least R nodes participating. So the maximum number of nodes that can fail and still allow a successful read is N-R.
Suppose we have a successful read and we now want to write the data. In order to perform a successful write we must have at least W nodes participating. So the maximum number of nodes that can fail and still allow a successful write is N-W.
And if you have no more nodes failing after the put() call, it is guaranteed that the W nodes that have successfully written the updated data are the highest W nodes in the priority list, which means that they will be selected in the next get() call, so you are guaranteed to get the latest version of the data.
The interesting thing here is that there's a fundamental trade-off between durability and availability. You can increase and decrease the likelihood of a failure of the first kind, but increase the likelihood of a failure of the second kind.
What's "eventual consistency", and what are some advantages and disadvantages? What's a specific example of behaviour that could happen under this consistency model?
Eventual consistency means that the database eventually reaches a valid state. I understand this as meaning that each of the N nodes must eventually hold the same copy of every key. More formally, there exists some time t in the future where such that for each key in each of the N nodes , each key's value is the same: that is, for each .
Advantages: you get asynchronous propagation. put() calls
are always available (provided you have at least W nodes),
subsequent get() calls can return without waiting for
put() calls to replicate themselves over N nodes,
which is good if or if we have server outages.
Disadvantages: subsequent get() calls are not guaranteed to
return the latest version of the data,
and reconciliation must be performed.
Specific example of behaviour that could happen under this consistency model: deleted items resurfacing in a "delete item from cart" if one chooses to merge the two different objects.
How does "consistent hashing" (compared to, say, ~hash(key) % N~) reduce the amount of data that needs to be moved when a node joins or leaves the cluster?
See front bit for the full explanation.
Where is the configuration information stored? How is it kept consistent?
It's kept by each node and kept consistent by gossiping.
Why is Dynamo only eventually consistent? How can divergent histories form even with a 3-2-2 quorum setup?
It would seem on the face of it that Dynamo can be completely consistent and histories can never diverge if one uses a 3-2-2 setup. Any write must have a quorum of two, and regardless of which two you choose (AB, BC, AC), they must have at least one node in common with the latest write, right? So how can inconsistency occur even in the presence of network partitions? The key (thanks Bernard) is that hinted hand-off loses consistency!
Recall that hinted hand-off allows nodes that are not in the first N nodes of the preference list to receive and temporarily store write requests for a node that's temporarily unreachable.
But this of course introduces inconsistency.
Suppose I make a write request.
I walk down the preference list to find the first two reachable nodes.
Suppose I get quorum from AB.
The vector clock looks like this: [SA, 1].
Then I make a second write request, and
let's say this time A was unreachable so I get quorum from BC instead.
C is updated with B's latest version of the data,
so everything is consistent.
We get ([SA, 1], [SB, 2]).
The second vector clock subsumes the first
so when A receives this new vector clock it knows to override its own.
But what if during the second write request A and B were both unreachable?
Then I would reach C, and by hinted handoff D would take over
keeping a message for A.
C would be holding a vector clock ([SC, 1])
and A would be holding the vector clock ([SA, 1]).
Now when A reconciles it has two different vector clocks
and no way to resolve them as they have nothing in common.
Questions in the lecture notes
Suppose Dynamo server S1 is perfectly healthy with a working network connection. By mistake, an administrator instructs server S2 to remove S1 using the mechanisms described in 4.8.1 and 4.9. It takes a while for the membership change to propagate from S2 to the rest of the system (including S1), so for a while some clients and servers will think that S1 is still part of the system. Will Dynamo operate correctly in this situation? Why, or why not?
Don't see why not: when S1 node is removed, S1 should offer and upon confirmation from the nodes clockwise to it transfer the appropriate set of keys. Call these nodes say S3, S4, and S5 given N=3.
One issue is if some nodes who think that S1 has been deleted contact the nodes in the new preference list who think S1 has yet to be deleted. So a node who thinks S1 has been deleted will contact S3, S4 and S5 for a write/read request. S3 and S4 will acknowledge and agree. However, S5 will believe it's not in its key range and will return false. But here there's still a quorum of 2 out of 3, and so there will be no problem in this scenario. Eventually the node removal will be gossiped to all alive nodes.
How does Dynamo recover from permanent failure -- what is anti-entropy using Merkle trees?
A: In this paper, anti-entropy is a big word for synchronizing two replicas. To determine what is different between two replicas, Dynamo traverses a Merkle representation of the two replicas. If a top-level node matches, then Dynamo doesn't descend that branch. If a node in the tree don't match, they copy the branch of the new version to the old one. The use of Merkle trees allows the authors to copy only the parts of the tree that are different. Wikipedia has a picture to illustrate: https://en.wikipedia.org/wiki/Merkle_tree.
Some deeper questions
Considerations/implications for database design?
- Is symmetry (lack of leader) important?
- Is it really important for every node to be able to service a write?
- Can you achieve low latency and high write availability with just one RW replica?
Acknowledgements
Thanks to Zongran, Bernard, Thomas, Gary, and Melodies for asking excellent questions and for answering them when I could not :P