Microeconomics Notes for Oxford PPE Finals
Fri Apr 16 2021tags: notes ppe oxford microeconomics economics finals
Introduction
These are notes I (Lieu Zheng Hong) wrote for myself while preparing for my Oxford PPE Finals. Some of my juniors asked for my notes and I am happy to oblige.
These notes are free to all but I ask that you do not reproduce them without first obtaining my express permission.
There are lots of mistakes, omissions, and inadequacies in these notes. I'd love your input to help make these notes better, by emailing me or by sending in a pull request at the GitHub repo here.
Table of contents
Some general thoughts
The situation for Micro is unlike that in Macro. There are a lot of excellent notes written by Bassel and others on the intuition behind general equilibrium, so these notes will be more exam-focused by giving the key definitions and how to solve problems.
Key definitions and questions to be clear about
What is the MRS?
- dU/dx / dU/dy = -dy/dx = - py/px
What is the MRT?
Slope of the PPF
In a competitive equilibrium with two goods and production, the MRS must equal the MRT !
Because the MRS is how much the consumer is willing to substitute one good for another, and the MRT is how much one firm can produce one good with another.
But check for corner solutions!
In a competitive equilibrium, a household maximises when MRS = slope of price line
THe price line is
General demands under a Cobb-Douglas utility function
In general, the share of the budget spent on a good is the weight placed on that good in the utility function. e.g. consider a market for apples, bananas and cherries. if consumer has an endowment of 10 apples and has utility function
his demands will be
General demands under a quasilinear utility function
You consume the concave good to the point where the marginal utility of the concave good equals that of the linear good, then henceforth you consume the linear good.
So you have for instance
What is a competitive equilibrium?
It is an allocation and a vector of prices such that: firms are producing according to their profit maximising function, consumers are consuming maximising their utility subject to their budget constraint, and all markets clear.
What are the key assumptions for a competitive equilibrium to exist?
- no frictions (no externalities, no tax distortions)
- no market power
- no uncertainty
- no increasing returns to scale (DRS or CRS only)
Draw an Edgeworth box for the exchange economy.
Draw a diagram of the Robinson Crusoe economy.
Draw an Edgeworth box for the economy with two factors of production and two firms (in K,L) space.
What is the slope/gradient of the price line?
What do the lines mean in the Edgeworth boxes?
What is the Stolper-Samuelson theorem?
Draw an Edgeworth box to illustrate the Stolper-Samuelson theorem.
What is Rybcynzki's theorem?
Draw an Edgeworth box to illustrate Rybczynski's theorem.
What does it mean for an allocation to be Pareto-efficient?
Does it make sense to say that a competitive equilibrium is Pareto efficient? Why or why not?
What is the Pareto set?
What is the Contract curve? How does it differ from the set of all Pareto-efficient outcomes?
What is the core?
(the set of allocations that cannot be blocked by any coalition of agents in the sense that they would increase their utilities by trading only amongst themselves)
What is the relationship between the Core, the Contract curve, and the Pareto set?
(The Pareto set is the set of all PE allocations. The contract curve in Alex's lectures is taken to be synonymous with the set of all PE allocations, but Bassel takes it to be the subset of the Pareto set that are Pareto-improvements over the initial allocation. The core is the See Bassel's notes for more details.)
The competitive equilibrium is always in the core.
In a large enough (replica) market, the only core outcome is the CE outcome.
What is the Edgeworth process?
(multiple rounds of decentralised trading between coalitions)
Does the Edgeworth process always converge to the core? Why or why not?
What is the UPF?
What is the First Welfare Theorem (FWT)?
If (x,p) is a competitive equilibrium, then THE ALLOCATION (not the equilibrium!) is Pareto-efficient.
What is the Second Welfare Theorem (SWT)?
If preferences are nonsatiated, any Pareto-efficient allocation can be supported by some price vector and transfers from an initial allocation .
Sketch out a proof of the FWT.
Suppose the competitive equilibrium was not Pareto efficient. Then there must be a feasible allocation such that is preferred to for some i. Then, for that agent i
and
(otherwise shecould have chosen x' from her endowment at competitive equilibrium prices). But then if we aggregate all the demands, it is clear that cannot actually be feasible.
Sketch out a proof of the SWT.
Draw an Edgeworth box to illustrate the FWT.
Draw an Edgeworth box to illustrate the SWT.
Draw an Edgeworth box to illustrate how taxing goods and giving the full
amount creates inefficiency (lecture 3 slide 26)
What is the tatonnement process? Describe it.
What are the two restrictions on aggregate demand in order for the tatonnement process to get us to the price vector that gives us the competitive equilibrium?
- gross substitutes
- WARP
What is the model of social choice?
(Individuals have a complete and transitive preference ordering over social states, which when aggregated form a preference profile (similar to a strategy profile). The social planner must find some way to aggregate these strategy profile into a societal ranking of social states)
What is a social choice rule?
(from a preference profile, produces a complete and transitive social ordering of social states)
What makes a good social choice rule?
- Unrestricted domain: social
- Pareto principle: if everyone prefers x
- Non-dictatorship
- Independence of irrelevant alternatives
What is a social choice function? How does it differ from a social choice rule?
(Social choice function selects one best social state)
What are the big answers in social choice?
- Arrow's theorem (1951) : Suppose there are at least three social states. Then there is no social choice rule which satisfies unrestricted domain, pareto principle, non-dictatorship, and IIA.
- Black's theorem (1948): If alternatives are one dimension and all voters have single peaked preferences, majority voting produces a social choice rule, and the majority of votes select the median alternative over another.
- What is liberalism? Respecting peoples' choices: for each player, there is at least one pair of alternatives and such that if is preferred by , then must be ranked higher than in the social choice function
- Sen's liberalism paradox
- Gibbard and Satterthwaite (1973, 1975): Suppose there are at least three social states. Then there is no social choice function which is strategyproof and respects citizens' sovereignty (every possible ranking of social states is possible for some preference profile)
What is Equivalent Variation (EV)?
income required at old prices to maintain new utility
What is Compensating Variation (CV)?
income required at new prices to maintain old utility (compensating you)
With quasilinear preferences, EV = CV = CS (as long as not a corner solution)
DWL is proportional to ad valorem tax * tax revenue
- More elastic demand or supply => higher DWL
- If demand is more inelastic than supply, then consumer bear most of the tax burden, and vice versa.
- Optimal taxation means taxing goods with higher demand elasticities less.
- Draw a diagram to show how public good underprovision occurs.
What is the Samuelson rule?
(The sum of marginal benefits of the public good must be equal to the marginal cost)
Explain why the Samuelson rule makes sense intuitively.
Explain the VCG mechanism. Give an example.
Give an example to show why the VCG mechanism is strategyproof.
What is a Pigouvian tax?
Show how setting price vs setting quantity can affect DWL when marginal benefit is uncertain.
Show how the deadweight loss is the same regardless of setting price v. setting quantity when the marginal cost is uncertain.
Under Cournot competition, what is the effect on the NE if the marginal cost of one firm decreases?
(BR curve shifts out, Firm 1 produces more, Firm 2 produces less, Firm 1 gains, firm 2 loses)
Under Bertrand competition with differentiated prices, what happens if both firms merge?
Prices increase as the firm takes into account the externalities of other's price
- What is the best-response curve for Bertrand competition with differentiated products? Show that it is increasing in the price the rival sets. (Makes sense --- you want to just undercut your opponent)
- Under Bertrand competition, what is the effect on the NE if the marginal cost of one firm decreases? (BR curve shifts out, Firm 1 prices higher, Firm 2 prices higher, both firms gain)
What are factors affecting the likelihood of collusion?
- Number of firms
- Real interest rate (or discount factor)
- Frequency of sales
- Ease of detection
- Cost of asymmetry (if firms have different costs, low cost firms have more to gain by deviating)
- Leniency programs
What is the Lerner index?
(P-MC) / P
What is the Herfindahl index?
(sum of squared market shares, in monopoly, 1, in oligopoly 1/n, in PC 0)
What is double marginalisation?
(When goods are complements, it's better for everyone (consumer AND producer surplus) if a single company sells all goods. Intuition: if there are multiple companies, each will try to maximise their profits by increasing the price, but they don't take into account the negative externality on demand on others)
Why is it sometimes bad to break up a vertical monopoly?
- Key factor: Whether products are complements or substitutes
- In concentrated markets where goods are complements, it may be better for everyone if a single company sells all goods
- Breaking up the firm does not increase competition when goods are complements!
- Intuition: If there are multiple companies, each will try to maximize their profits by increasing the price
- But if they don’t take into account the negative impact on volume for others, then they will overcharge
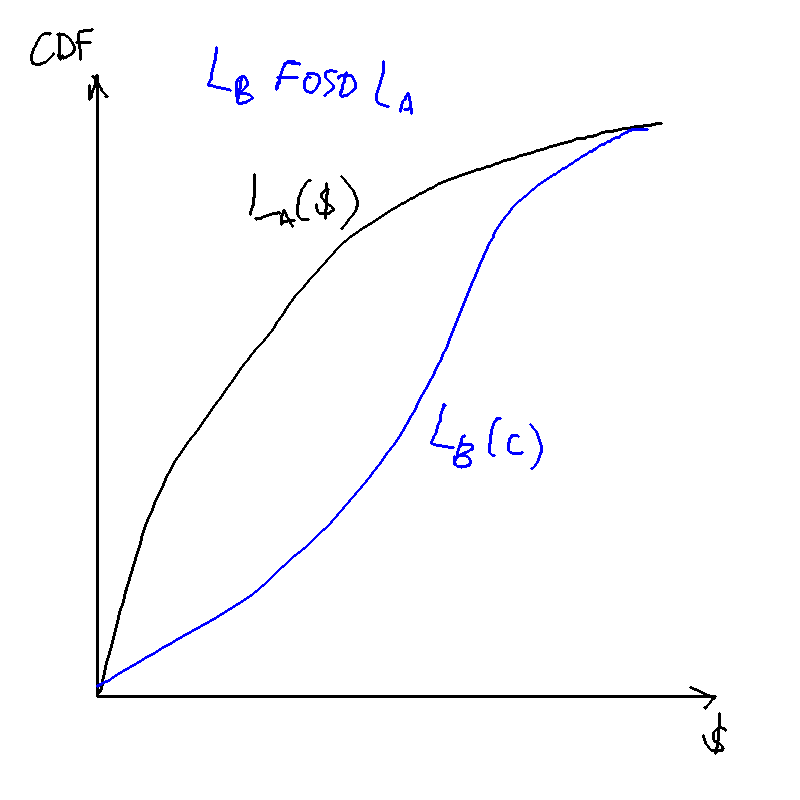
What does it mean for a lottery to FOSD another?
A lottery first-order stochastically dominates another if for every outcome , the probability of getting at least is higher under than .
First order stochastic dominance: would every expected utility maximiser prefer a lottery to ?
A necessary and sufficient condition for one lottery to FOSD another is if the CDF of that lottery lies below the CDF of . That is, if the probability of lower outcomes is always lower under than .
What does it mean for a lottery to SOSD another?
Would any risk-averse or risk-neutral utility maximiser (weakly) prefer it?
A lottery second-order stochastically dominates another if the area under the cumulative distributive function of lottery is less than the area under the cumulative distributive function of lottery until we reach the best outcome.
Second-order stochastic dominance: would every risk-averse utility maximiser choose the lottery over another?
FOSD is a stronger condition: if a lottery FOSDs another, it will definitely SOSD it too. However, a lottery that SOSDs another will not FOSD another, as risk-loving types prefer a higher variance.
If SOSD then the expected value of must be equal or higher than , , and for risk-averse types, .
What's the difference between risk pooling and risk sharing?
What is the slope/gradient of the isoprofit line?
What is the gradient of the indifference curve in the state-space diagram?
On the certainty equivalent on the state-dependent diagram, why is the gradient of the indifference curve ?
Why is there no pooling contract in the insurance market with unobservable types?
What is absolute risk aversion?
The Arrow-Pratt coefficient of absolute risk aversion is
What is relative risk aversion?
The Arrow-Pratt coefficient of relative risk aversion
What is the certainty equivalent?
The certainty equivalent is the outcome that would give the equivalent utility of the above lottery: that is,
What is the risk premium?
The risk premium associated with a lottery is the difference between the expected value of the outcome, and the certainty equivalent:
How can we calculate the risk premium without calculating the CE?
It can be shown that a lottery with "small" gambles, the risk premium is given (approximately) by
where is the variance of the outcomes. Equivalently,
What is CARA, CRRA, DARA?
An example of a utility function with constant absolute risk aversion (CARA):
Constant relative risk aversion (CRRA):
Note that since , CARA imples IRRA and CRRA imples DARA.
Why does CRS mean 0 profit and DRS means positive profits in eqm?
In CRS. Suppose we've optimised and , and we are making positive profits . But then we can simply scale all inputs by , and make even more profits, ad infinitum, unless your profits are zero.
In DRS, the worker is paid extra wages up until wage equals marginal cost
MRS: slope of indifference curves MRT: slope of PPF
What is the fair insurance condition?
where the probability of accident is and the premium is purchased at .
What is agency loss/agency cost?
Agency loss is the difference between the expected wage and the certainty equivalent.
Entirely equivalently, agency cost is defined as the difference in expected surplus to the principal under unobservable vs observable effort.
What is premium? How does it differ from premium rate?
Premium is the expected loss P, premium rate is what you pay per unit of cover.
General Equilibrium
The big picture
The key idea is that we define this notion of a "competitive equilibrium", which is an allocation of goods and a vector of prices such that:
- Consumers maximise utility subject to budget constraints
- Firms maximise profits
- All markets clear
For condition 1, we need the Lagrange, the Kahn-Tucker conditions, and the Envelope Theorem.
For condition 3, this requires that excess demand for each good equal to zero
Finally, we bring in welfare. We bring in the concepts of Pareto-Efficiency, Kaldor-Hicks efficiency, x Pareto-dominating y, contract curve
Contract curve: traces out the set of points that an agent would be willing to move to (the set of Pareto-improving points from a person's initial endowment).
- What do different contract curves look like for different utility functions?
- Quasilinear utility functions:
and we have some key results: the first and second welfare theorem
- FWT: all CE are PE
- SWT: any PE can be supported by a price vector that is a competitive equilibrium.
Bassel says: Outline how the proof works for both FWT and SWT, and have a neat diagram (Edgeworth Box) prepared.
Assumptions:
- FWT requires some assumptions
- SWT requires some assumptions AND assumption of convex indifference curves
- take a point that is PE.
- Find the MRS that slices through the two indifference curves. This is the price line
- Find a lump-sum transfer, and set some price vector, that brings us from the original point to the desired point.
(Question: if you can do unrestricted lump-sum transfers, why not just transfer directly to the desired point?)
(Answer: Some goods may be difficult to transfer)
Bassel says: Talk about the definitions and implications of FWT and SWT. Good for essay questions.
Bassel says: This whole notion of competitive equilibrium doesn't have any thing about how people trade and get to that point. That's why we have tacked-on a Tattonment process, or reaching a price vector through bartering
The Edgeworth process gets you to a PE (on the contract curve), but not necessarily the specific CE supported by the price vector.
Bassel says: For an essay on general equilibrium, clarity is key. Nail down all the definitions, have a very clear struture of the essay, relate the concepts to one another in a clear way. Don't mix up questions on existence to questions on efficiency to questions on price.
Prepare chunks of essays, if I need to write on FWT/SWT, exchange economies, etc.
The only difference between autarky and trade is that the market clearing conditions are different.
One wage that clears one market for labour.
If no free mobility, then you have two wages
TODO
- draw diagrams for exchange economy
- draw diagram for robinson crusoe eocnomy
- draw out diagrams for the stolper-samuelson theorem and rybcyznski theorem
- draw diagrams for how trade improves the economy
- draw a diagram for how trade may affect consumers with heterogeneous preferences
- Draw an Edgeworth box to illustrate the FWT.
- Draw an Edgeworth box to illustrate the SWT.
- Draw an Edgeworth box to illustrate how taxing goods and giving the full amount creates inefficiency (lecture 3 slide 26)
- draw diagram to show EV vs CV (lecture 6)
- Draw a diagram to show how public good underprovision occurs. (7)
Optimisation
MRS
For any utility function u(x,y) the MRS gives the slope of the indifference curves in (x,y) space, and can be found as follows:
With quasilinear preferences,
and
which depends only on y.
This means that the marginal rate of substitution is always constant at any value of x. Meaning to say if you draw a horizontal line, the points that cut the horizontal line will always give you the same MRS.
Hicks demand v Marshallian demand
Marshallian demands are "proper" demands, or demands that optimise the quantity of good demanded subject to their budget constraint.
Hicks demands are "cost-minimisation" demands
Kuhn-Tucker conditions
The Kuhn-Tucker conditions give us the first order conditions for an optimum when using the Lagrangian to solve a constrained optimisation problem.
See Bassel's notes, 1 Constrained Optimisation
Envelope Theorem
See Bassel's notes, 1.5 The Envelope Theorem
Interpretation of the Lagrangian multiplier
The Lagrangian multiplier measures the change in the optimised value of the objective when we marginally relax the constraint.
For regular consumer optimisation
the Lagrange multiplier is the marginal utility of income. (When we marginally increase income, what is the change in the utility?)
Quasilinear preferences
where is an increasing concave function.
The key property of quasilinear preferences is that the indifference curves will have the same slope along any line that is parallel to the axis on which the "linear" good is drawn.
Cobb-Douglas preferences
Homothetic: the slope of indifference curves is the same throughout any ray that passes through the origin.
Edgeworth boxes
Offer curve
- Offer curve
- Pareto set
- Contract curve
Contract curve
The contract curve is the set of all Pareto-efficient allocations that give a higher utility to everyone compared to the endowment point.
Pareto set
Consider two agents with the same utility function
Now consider two agents with different utility functions:
Contract curve will "curve" towards A, giving more of good Y to A
Bassel says: Keep this in mind. The minute you see what the utility functions are like, that tells you what the contract curves will look like. e.g. In any competitive equilibrium, A will get a higher relative ratio of good Y/good X than B.
It will always go halfway up the y axis
You want to consume y infinitely more when y is at zero nuntil 1, and when you have more and more of y, the additional value gets lower and lower until it reaches less. After a certain point, you only want x.
So you want all of Y until a certain point, then you only want X.
Income expansion path: keeping the same price level (gradient of the graph), what is the quantity of x and y demanded?
With different quasilinear preferences, the line shifts up
...
Competitive equilibrium
Walras's Law
The sum of the value of the excess demands must equal zero.
Excess demands are defined by the excess goods demanded, so the value is multiplied by the prices
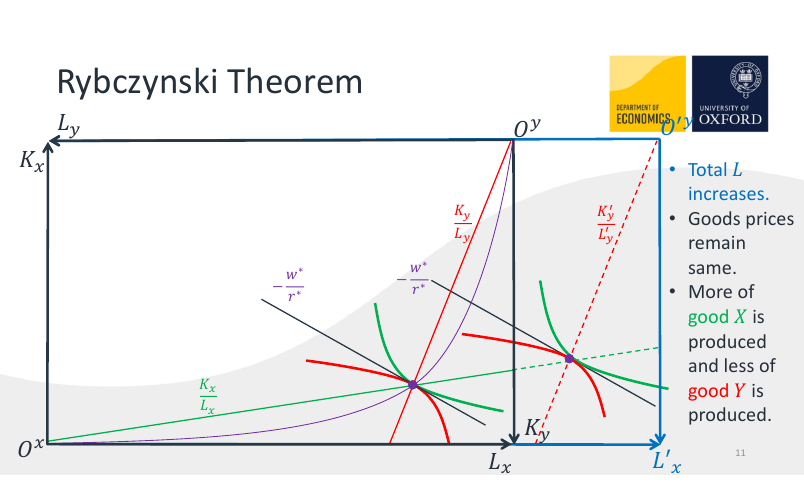
Rybczynski's theorem
Consider an economy with two goods being produced with two factors of production.
The theorem states that an increase in the supply of one factor will increase the output of the good that utilises that factor more. For instance, if there are two factors of production, labour and capital, and there are two goods, haircuts (labour-intensive) and skyscrapers (capital-intensive), then the equilibrium output of haircuts will increase if the supply of labour increases.
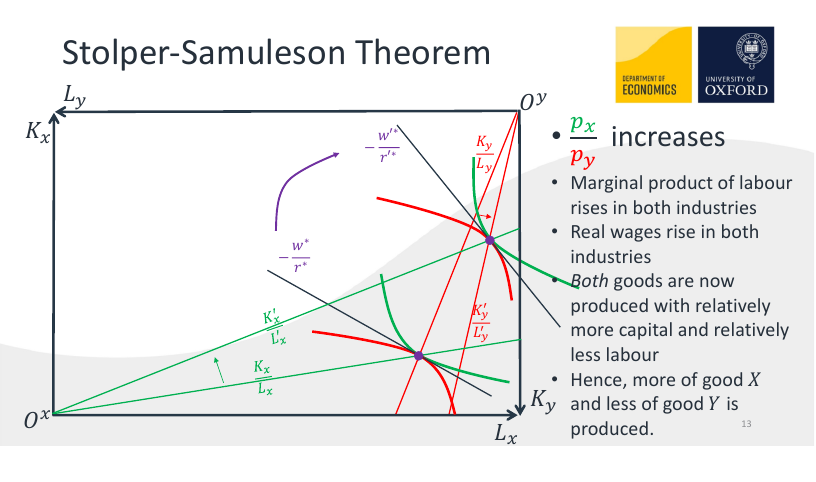
Stolper-Samuelson theorem
Again, consider an economy with two factors of production and two goods being produced, one of which is capital- and the other labour-intensive.
An increase in the relative price of a good will cause the real return of the more intensive factor to increase, and decrease the real return of the less intensive factor.
Welfare Economics
- First Welfare Theorem
- Second Welfare Theorem
Consumer optimisation
Bassel's notes are great for this.
Assumptions of general equilibrium
- No frictions
- No externalities
- No distortionary taxes
- No market power (price-taking firms)
Types of general equilibrium
- Exchange economy (two goods, two people with endowments)
- "Robinson Crusoe" economy: (one producer, one consumer, one good, one factor of production)
- An economy with one producer, one consumer, one good, but two factors of production.
- 2x2 (multi-industry) economy: two goods being produced, two factors of production, two (types of) companies
How to solve general equilibrium questions
The key is to ask yourself the following: What are the goods and what are the markets? Then you'll know what needs to clear in equilibrium.
In the simplest case of an exchange economy, there are two goods and two agents, then you'll need to have 2x2 = 4 equations, and there are 4 unknowns: . Once we have the four demand equations (each agent's demand for each good), we can then find the prices that will clear the market, and the equilibrium allocation of goods x and y that will result.
Two market clearing conditions:
In the case of a "Robinson Crusoe" economy, there are two goods, (the consumption good) and labour . There are two agents, and two prices and . The firm has its own production function, the consumer has his demand function. From here we can get the four equations:
- firm's demand for labour,
- firm's supply of good,
- consumer's supply of labour,
- consumer's demand of good.
Four equations, four unknowns. Again, same thing, plug in to find the prices, then use the prices to find the eqm allocations.
In the case of an economy with two firms and only one factor of production, there are the goods , , the factor of production , the prices , , and .
Seven equations:
- firm 1's demand for labour,
- firm 2's demand for labour,
- firm 1's supply of x,
- firm 2's supply of y,
- consumer's supply of labour,
- consumer's demand for good x,
- consumer's demand for good y.
We have seven unknowns (we need to know how demand is split between two different firms and the consumer):
In the case of an economy with two factors of production, there are three goods: , , and and three prices , , .
There are six equations:
- firm's demand for labour,
- firm's demand for capital,
- firm's supply of good x,
- consumer's supply of labour,
- consumer's supply of capital,
- consumer's demand of good x.
Six equations, six unknowns. Solve to find relative prices, and then plug them back into the demand and supply functions to find the equilibrium allocations of labour, capital and good x, and the price vector that clears the markets.
In the case of a multi-industry economy, there are two goods, and , two factors of production and , two rental rates and , and two prices and . (We ignore the consumer in this case.) The equations are:
- firm 1's demand for labour,
- firm 1's demand for capital,
- firm 1's supply of good X,
- firm 2's demand for labour,
- firm 2's demand for capital,
- firm 2's supply of good Y,
- consumer's supply of labour,
- consumer's supply of capital,
- consumer's demand for good X,
- consumer's demand for good Y.
The unknowns are . (this seems to deviate from the treatment in the lectures though. Ask Bassel tomorrow. He might point me to Mas-Colell.)
Here is the "cookbook approach to finding a competitive equilibrium" in Alex Teytelboym's lecture notes:
- Find the demand and supply functions of each agent and for every good as if it’s partial equilibrium.
- Make sure that these demand and supply functions are only functions of prices. So, for example, get rid of “endowment”
- For each good in the economy, calculate aggregate demand, aggregate supply, and aggegate endowment. Together they give you an excess demand equation that should be zero in equilibrium.
- Now, you have a market-clearing condition for every good: k equations and k unknowns. Existence theorem tells that a solution exists (phew). And you only need to solve k - 1 such conditions by Walras’s Law.
- Solve to find relative prices. Sometimes it helps to fix the price of one good at, say, 1 and solve prices with this good as numeraire.
- Once you’ve found the equilibrium prices, plug them back into the demand and supply functions to find the equilibrium allocation. Remember to specify the equilibrium allocation (x in the exchange economy or (x, y) in production economy) AND the equilibrium price vector p.
Pure exchange economy
Consider a pure exchange economy with two consumption goods, 1 and 2, and two consumers, A and B. Consumer has an endowment of 10 goods of unit x, consumer has an endowment of 10 goods of unit y, and let the price of good 1 be normalised to 1 and the price of good 2 be .
Taking their utility functions to be
let's write out the four equations and unknowns.
We need to know:
- A's demand for X;
- A's demand for Y;
- B's demand for X;
- B's demand for Y.
We need to find the price vector that clears the market. The market clearing condition is that the demands must sum up to the supply.
To do this, let's solve the Lagrangian for consumer A. He has an endowment of 10 of good X, worth 10 dollars in total. So:
The Kuhn-Tucker conditions give us:
We solve and obtain the conditional demands, with both player 1 and player 2. These are the quantities each player will demand as a function of the price .
We have obtained the demands. But there will be excess demand unless we set the correct prices. We know that in order for all markets to clear (we only need to clear the market for good x in order for the market for good y to clear as well). So it's clear that must equal 1.
Now that we've found the price vector, we can simply plug this price vector back into the conditional demand to get the actual allocations. The competitive equilibrium is thus
That was how we solved the most basic general equilibrium problem.
"Robinson Crusoe" economy: economy with one consumer, one producer
"Robinson Crusoe" economy with income taxes
In general equilibrium, the taxes have to go back to the consumer.
Normalise the price of good C to 1. The optimisation objective of the consumer is to maximise subject to
Note that is in the tax term, you take it as given by getting a percentage of all tax receipts.
Let the functions be
Claim (verify for tomorrow):
At the optimum,
Economy with one factor of production but two firms
Economy with two factors of production and one firm
2x2 economy (two goods produced)
See 2016 Q8.
OK, so these are the conditional factor demands for the wage rate and the output chosen and . How do we get the actual factor demands?
We need to do a profit maximisation equation and find the quantity of and produced, in order to know how much , , and is demanded.
And then we know that markets have to clear, so and .
So here we have the following unknowns:
And we have the following equations:
And the market clearing conditions
Markets have to clear
So now we have to solve and such that the markets clear. How? Or is it solving and such that the markets clear?
We have as functions of , the factor price ratio. Are we done? Not yet, I think we still need to find it in terms of p1 and p2. After that is done, I think we will have the equilibrium: we have found the price vector p1 and p2 that results in the labour and capital markets clearing.
Economies with trade
One factor of production (L), but two goods and . To make things easier, we assume the consumer derives no utility from leisure, so they always provide 1 unit of labour at the wage . We thus get six equations and six unknowns:
- firm 1's demand for labour,
- firm 2's demand for labour,
- firm 1's supply of good x,
- firm 2's supply of good y,
- consumer's demand for good x,
- consumer's demand for good y.
Now fix the wage level . For every relative price level we will get a different level of production of good x and good y. This is basically the PPF:
Edgeworth boxes in trading economies
[TODO]
Instead of indifference curves, we have isoquants, and the rays shooting out of the origins denote the conditional factor demands. That is to say, at a certain price level, what is the optimal amount of each factor and I should use?
Welfare Economics
VCG mechanism
Suppose the government wants to build a bridge at a cost of $1000.
The government asks each person to report their benefit from the bridge. In order to keep people honest, the idea is: the more you report, the more you pay, but only if you are pivotal.
What you pay is the following: you pay the difference in:
Net utility if everyone except you participated - Net utility of everyone else except you when you participate
As an example, consider three agents with reported utilities
Since , the government builds the bridge.
For agent one, the net utility if everyone except him participated would be zero, as the bridge would not be built (he is pivotal). So he pays 0 - (900-1000) = 100.
For agent two, the bridge would still be built, so the net utility in both cases is 200, so he pays nothing.
Agent three is pivotal, so he pays 0 - (700-1000) = 300.
However, total tax collected is only 400, which is not enough to pay for the bridge! In general, there cannot exist a strategyproof mechanism that is budget balanced and also ensures payoffs > 0 for each player.
The government can coerce people to participate, so the last impossibility condition may not bite.
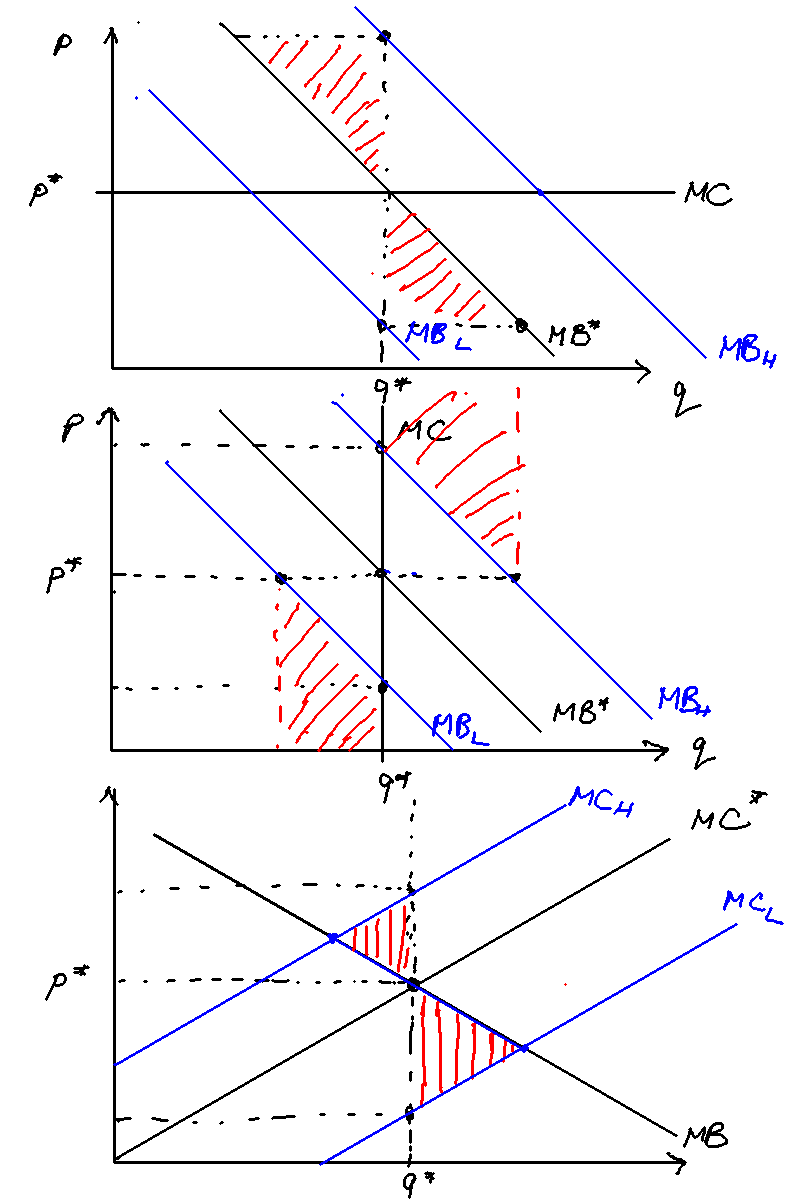
How uncertainty affects the choice of targeting price vs quantity
Set-up: the firm produces at its private marginal cost PMC, and gains some marginal revenue from selling a good MB. But it also imposes a societal marginal cost, SMC, on society. It thus overproduces the good.
There are two ways to get the societally optimal level of production: one, set a quantity cap: two, set a Pigouvian tax that increases the private marginal cost to match the societal marginal cost. The equivalence of price and quantity means that we can reach the societally-optimal level with either approach.
But what if there is uncertainty about either the marginal benefit or marginal cost of the externality? If so, taxation vs quotas can have different consequences. The headline results are as follows:
- Under uncertainty over marginal benefit, a flat marginal cost curve means that choosing taxes over quotas is better (results in less DWL).
- Under uncertainty over marginal benefit, a steep marginal cost curve means that choosing quotas over taxes is better (results in less DWL).
- Under uncertainty over societal marginal costs, setting quotas or taxes result in the same amount of deadweight loss, so it doesn't matter.
The intuition is as follows: A firm's choice of production depends only on its private marginal benefit and marginal costs. The uncertainty in marginal costs will not affect the firm's choice of output. In contrast, uncertainty in marginal benefits either changes the equilibrium output (under taxes) or not (under quotas) which can result in different deadweight loss depending on the slope of the SMC curve.
Setting a price is essentially setting a horizontal line equal to MC at that point. When the marginal cost curve is flat, a big change in quantity produced actually only deviates from the societal optimum a tiny amount. Figure \ref{welfare_under_uncertainty} illustrates.
Risk and Expected Utility
A lottery is a list of pairs, one per state, each comprising a probability and an outcome:
Consider a lottery with two possible outcomes and , with probabilities and . Denote the expected value of the outcome as and the expected utility, , as .
Certainty equivalent and risk premium
The certainty equivalent is the outcome that would give the equivalent utility of the above lottery: that is,
The risk premium associated with a lottery is the difference between the expected value of the outcome, and the certainty equivalent:
What does it mean to be risk-averse?
Someone is risk-averse if any of the following are true (the definitions are equivalent):
- The utility function is concave
- The certainty equivalent is less than the expected value of the outcome
- The risk premium is positive.
Absolute and relative risk aversion
The Arrow-Pratt coefficient of absolute risk aversion is
and it can be shown that a lottery with "small" gambles, the risk premium is given (approximately) by
where is the variance of the outcomes.
The Arrow-Pratt coefficient of relative risk aversion
With small gambles, the risk premium is given approximately by
An example of a utility function with constant absolute risk aversion (CARA):
Constant relative risk aversion (CRRA):
Note that since R(y) = A(y)(y), CARA imples IRRA and CRRA imples DARA.
Drawing indifference curves
We draw indifference curves of the form
for some constant and is the probability of outcome occurring. Usually when we draw these indifference curves
The slope of the indifference curve,
and the derivation is in Bassel's notes. Along the certainty line, the slope of the indifference curve is exactly , because the income amounts are the same.
The certainty equivalent of a lottery is the point C where the indifference curve through cuts the certainty line.
Additionally, to find , or the expected income, we know that
and so the slope of the iso-income line is simply given by
by the chain rule.
The risk premium is therefore , which is on the graph.
First and second-order stochastic dominance
A lottery first-order stochastically dominates another if for every outcome , the probability of getting at least is higher under than .
First order stochastic dominance: would every expected utility maximiser prefer a lottery to ?
A necessary and sufficient condition for one lottery to FOSD another is if the CDF of that lottery lies below the CDF of . That is, if the probability of lower outcomes is always lower under than .

A lottery second-order stochastically dominates another if the area under the cumulative distributive function of lottery is less than the area under the cumulative distributive function of lottery until we reach the best outcome.
Second-order stochastic dominance: would every risk-averse utility maximiser choose the lottery over another?
FOSD is a stronger condition: if a lottery FOSDs another, it will definitely SOSD it too. However, a lottery that SOSDs another will not FOSD another, as risk-loving types prefer a higher variance.
If SOSD then the expected value of must be equal or higher than , , and for risk-averse types, .
The idea of a "mean-preserving spread": something that maintains , but "spreads" the probabilities out so that you are more likely to get very high or very low values.
For instance, let the outcomes be , and the lotteries be . Here SOSDs because the means are the same but the chances of getting a lower outcome in are higher. We can draw the CDFs:
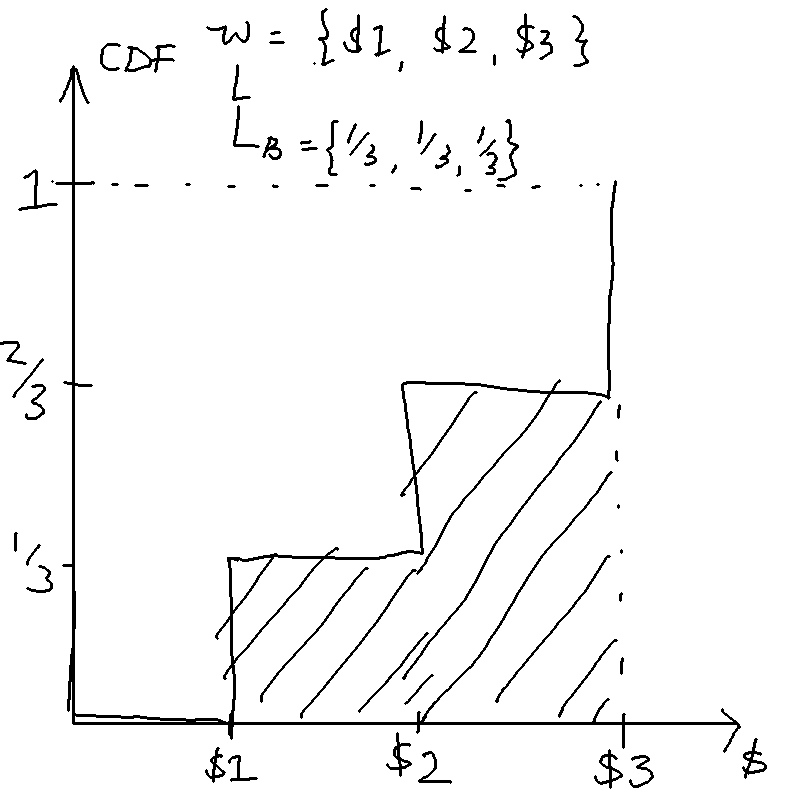
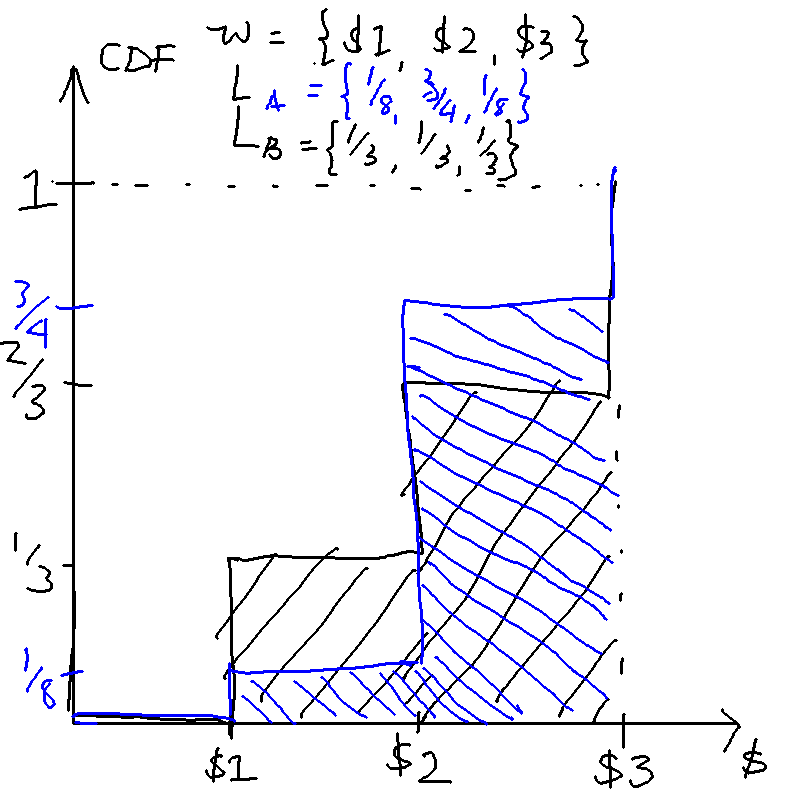
Risk-pooling and risk-sharing
The difference between risk-pooling and risk-sharing is that risk-pooling is about taking multiple independent risks, while risk-sharing is taking one risk but dividing the payoffs between people
Insurance
The agent can be in no accident state or an accident state . Let the probability of accident be and no accident .
The agent can purchase a premium from the insurance company at rate . In the no-accident state, the agent gets but has to pay a premium . In the accident state, the agent loses , but gets compensated from the insurer, so he obtains .
The agent's utility is thus
where
Rearranging and eliminating we obtain the budget constraint in state-dependent preference space,
Insurance is actuarially fair if the value of the premium is equal to the expected claims (insurance companies make zero profit). The company's expected profit is
If insurance is actuarially fair, the agent fully insures: they buy enough cover such that they get the same payoff in either state. The indifference curve has a slope of when it passes through the certainty line, while the insurance line (the line whereby the insurance company makes no profit) is has a slope of .
The slope of the consumer's indifference curve is gotten in a similar manner to the MRS. We have the utility function
Taking the total derivative and setting it to zero we have
Rearrange to get
Fair insurance condition:
[Image in Bassel's notes]
If insurance is actuarially unfair, the agent doesn't fully insure: the slope of the isoprofit line of the insurer swivels counterclockwise, and the agent purchases some level of insurance that maximises his utility.
[Image in Bassel's notes]
Insurance
A zero-profit pooling equilibrium cannot be possible if types are unobservable. This is because suppose a pooling equilibrium existed. Then an insurer can offer a cheaper premium that will be taken by low-types only, and would also make positive profit. (There is a pooling equilibrium with positive profit, though --- or is there? Ask Bassel)
When types are unobservable, there can be a separating equilibrium giving both a fair price, but giving only partial cover to the low-types. This partial cover must be such that it lies below the indifference curve of the contract offered to high-risk types.
There may not always be a separating equilibrium. It depends on the proportion if H-type to L-types. If the proportion of low-risk types is high, then the pooling equilibrium zero profit line is close to that of the L-type zero profit line, very steep. (Remember, the steeper the zero profit line, the lower the premium.) There would thus be an incentive to offer a partial pooling contract that would make a positive profit.
It's a bit odd that there is no pooling and there may not be a separating equilibrium. In fact, there is a symmetric mixed equilibrium, no pure equilibrium necessarily exists. See Bassel's notes.
Separating vs pooling equilibrium
PYP 2017 Q9: should an agent buy unfair insurance, and how should insurance companies serve both low-risk and high-risk individuals?
Hugh believes that he is low risk – he locks windows and doors when he leaves home, and he doesn’t leave candles burning when he goes to bed. He faces insurance that is actuarially unfavourable, and so decides not to buy any. Is he acting optimally? How might competitive insurance companies overcome the problem of serving both low risk and high risk individuals?
Whether or not Hugh should buy insurance depends on how actuarially unfavourable the insurance is. If the insurance is somewhat actuarially unfair, Hugh should buy some insurance but not fully insure. But if the insurance is very actuarially unfair, Hugh is acting optimally in not buying any insurance. I will illustrate this with the help of three state-space diagrams. Competitive insurance providers can serve both low- and high- risk individuals by offering two different contracts: one high-priced full coverage, the other low-priced with partial coverage. However, whether or not this is an equilibrium depends on the proportion of high- and low-risk individuals. A separating equilibrium can only obtain if the proportion of low-risk individuals is not too high.
I first set up the insurance model. We model Hugh as an expected utility maximiser who is somewhat risk-averse. Hugh has some starting wealth . There is some probability of an accident happening with probability , whereupon he incurs some loss: his new wealth is . Hugh's expected utility is thus
We can represent the two possible states of Hugh's wealth in a state space diagram. The state space diagram represents Hugh's expected utility in different possible lotteries that he faces. The x-axis represents his wealth in the no-accident state, while the y-axis represents his wealth in the accident state. We can also draw an indifference curve, which represents the set of lotteries Hugh is indifferent between. Importantly, the 45 degree line represents no lottery at all.
With the state space diagram, we can now see whether Hugh should buy insurance.
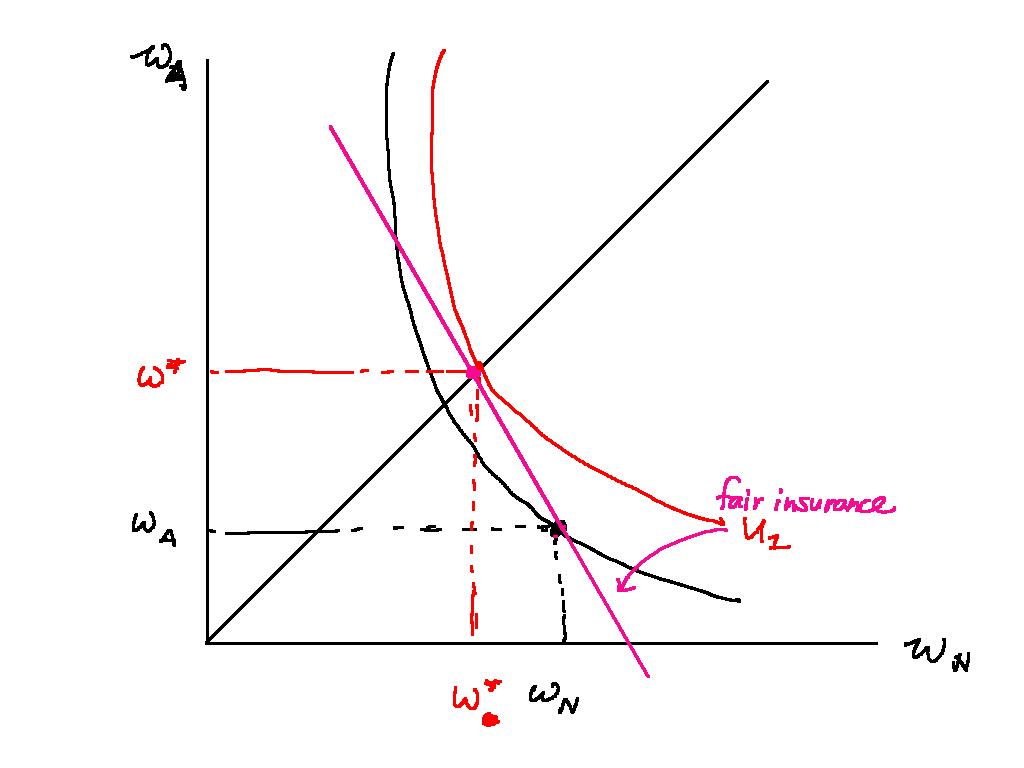
Hugh has the option to purchase insurance with a cover of q and a premium per unit of cover.
Figure \ref{fair_insurance} shows insurance that is actuarially fair. Insurance is actuarially fair when the company makes zero expected profit: that is, when
This means that , or the premium per unit of cover is exactly equal to the chance of an accident. When this is the case, Hugh should fully insure such that he loses nothing in the accident case.
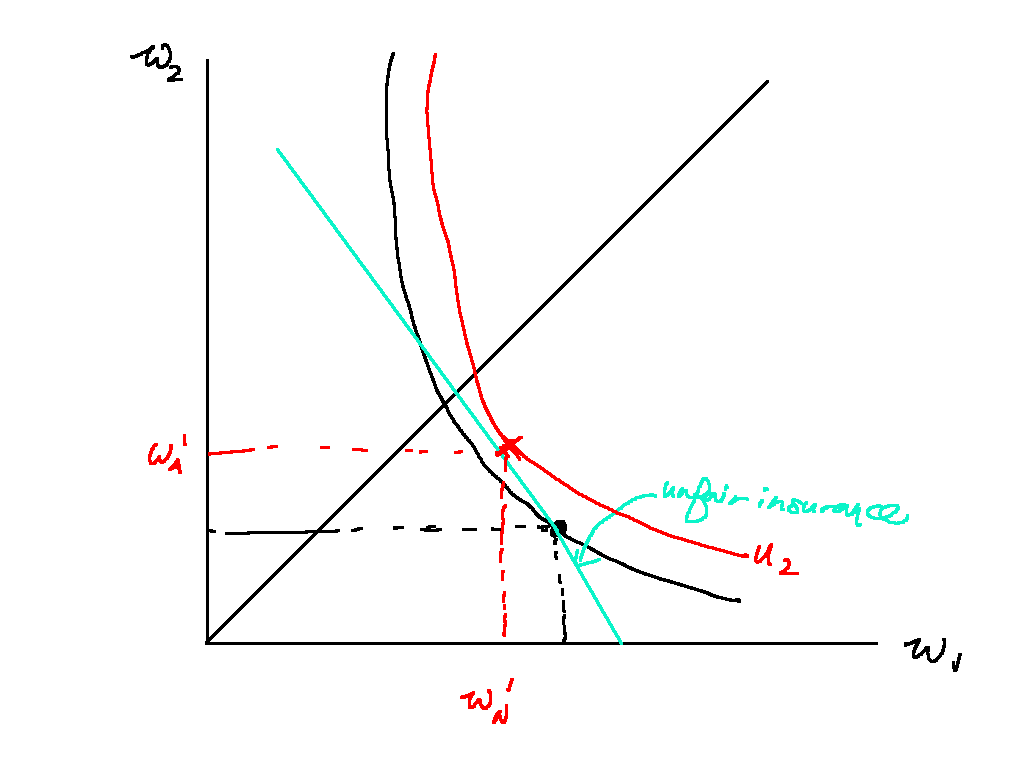
Figure \ref{unfair_insurance_1} shows how Hugh should still purchase insurance even if it is not actuarially fair. Here the company is offering cover at a higher premium , which translates to a flatter slope. However, Hugh should still purchase some insurance as purchasing some insurance will move him to a higher indifference curve in red, compared to his original lottery.
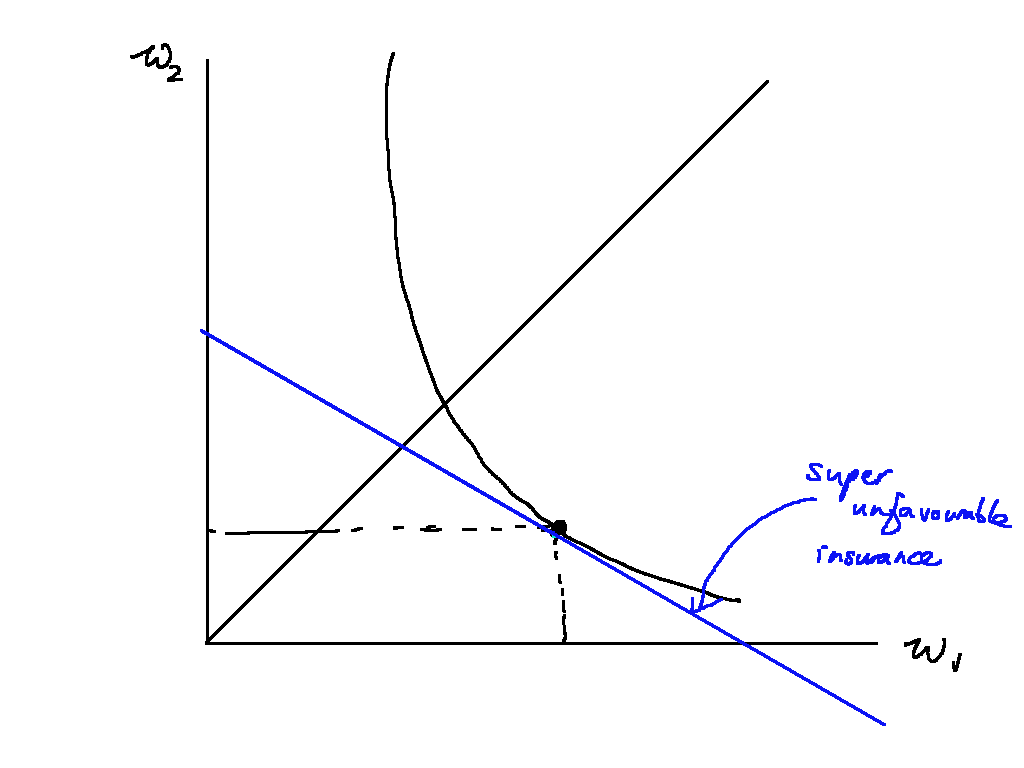
Finally, Figure \ref{unfair_insurance_2} shows that Hugh should not purchase any insurance if the premium is too high. In the figure, the premium is so high that Hugh would be on a lower indifference curve if he bought any amount of insurance. In this case, it is optimal not to insure.
Overall, therefore, whether Hugh is acting optimally depends on the price of his insurance. The slope of his indifference curve is given by
and thus if is greater than , it is not optimal to buy any insurance.
We now move on to how competitive insurance companies might overcome the problem of serving both low- and high-risk individuals. Competitive insurers must make exactly zero profits on both high and low-risk agents. But
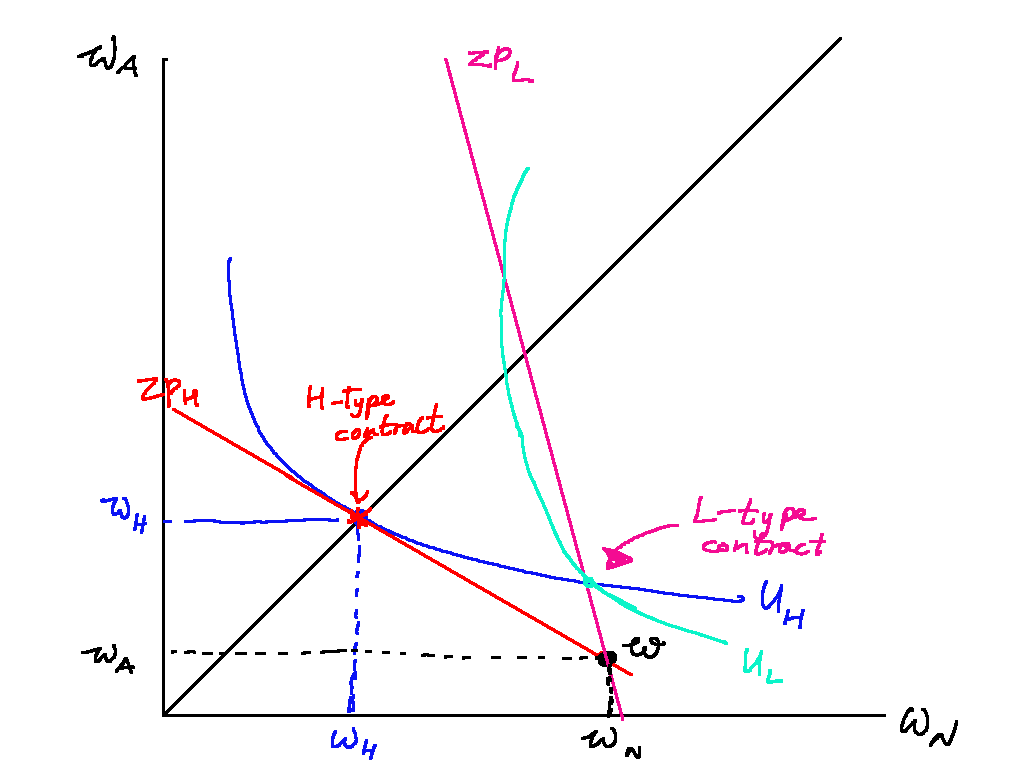
The trick is therefore to offer partial cover with a low premium to low-risk types like Hugh, and full cover with a high premium to high-risk types. Figure \ref{sep_eqm} illustrates. Both types initially face different lotteries but with the same outcome or , denoted as in the state-space diagram.
The insurance company offers two contracts: one full-coverage at a high premium (in red), and one partial coverage in pink . Importantly, the insurer cannot offer full coverage to the low-risk type, because then the high-risk types would take it up. In this case, the partial coverage means that H-types prefer the contract meant for them, as the partial coverage lies below their current indifference curve on the high contract.
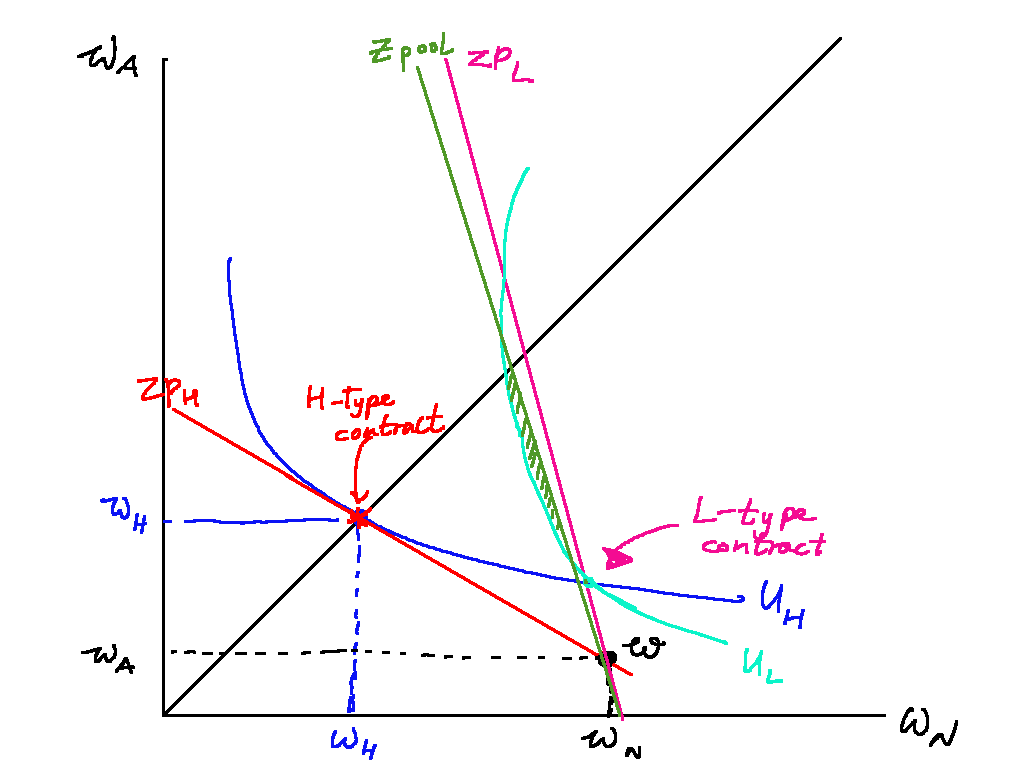
However, this separating equilibrium may not exist. If the proportion of low-risk types is large enough, there is a profitable deviation for insurance companies to offer a pooling contract anywhere in the shaded region below the zero-profit pooling line (in green). This deviation will be profitable as it lies below the zero profit line, and both high-risk and low-risk types will switch as any point in the shaded region lies above the current indifference curves for both high- and low-risk types.
\pagebreak
Principal-agent problem
Suppose a risk-neutral principal derives a payoff which depends on output, which in turn depends on the effort exerted by the agent.
The agent's utility function is some function of his wage minus his effort cost:
We assume that effort can only take low or high levels: that is, .
Let the probability of a "high" outcome conditional on the agent exerting effort level 1 be denoted as , mutatis mutandis for effort level 0. That is, and . Additionally, we demand that .
The principal wants to maximise his expected profit by choosing a contract which induces an effort level so as to maximise the following profit function:
The agent has both a participation and an incentive constraint. The participation constraint ensures that the agent's reservation utility must be lower than his wage when he exerts either high or low effort, i.e. it is better to work than not at all. The incentive constraint is that , i.e. it's better to exert high effort than low effort.
The incentive constraint can be written as follows:
The agent will prefer to exert high effort to low effort when the expected utility from high effort exceeds the expected utility from low effort.
To induce high effort, the principal must offer a low wage that is low enough to satisify the incentive constraint. We rearrange the incentive constraint and take inverse function on both sides to obtain
It must also offer a wage high enough to satisfy the participation constraint:
Agent is risk neutral
Effectively set b=1 since risk-sharing is not a concern.
Agency cost
Agency cost is defined as the difference in expected surplus to the principal under unobservable vs observable effort.
2016 PYP: Reference essay for principal-agent problems (all cases)
A risk-neutral principal wants to hire an agent to undertake a project. What considerations does the principal take into account when designing the optimal contract? (For illustration purposes, you may assume that there are just two possible levels of gross profit, and two levels of effort that the agent can exert.) Compare the optimal risk-sharing contracts when effort is observable and when it is not: if the principal wants to induce different effort levels in these two situations, who is better or worse off? If on the other hand the principal wants to induce the same effort level in these two situations, is anyone better or worse off?
Introduction
In every case, the contract offered to the agent must satisfy the participation constraint: the contract must be attractive enough to the agent for it to take up the contract. Additionally, when the agent is risk-averse and effort is unobservable, the agent will also need to satisfy the incentive-compatibility constraint: the expected utility accrued to the agent must be greater when exerting the desired level of effort. In this essay, I set up the basic principal-agent model and lay out the PC and IC. I show that the principal is worse off in two cases: 1) when the principal wants to elicit high-effort regardless of observability; 2) when the principal wants to elicit high-effort in the observable state but low-effort in the unobservable state.
Basic model set up
Suppose a risk-neutral principal derives a payoff which depends on the output level , and the state-dependent wage it pays to the agent . The output level in turn depends on the agent's exerted effort. Here we assume that effort can only take low or high levels: that is, .
Let the probability of a "high" outcome conditional on the agent exerting effort level 1 be denoted as , mutatis mutandis for effort level 0. That is, and . Additionally, we demand that : if the agent exerts high effort, the probability of a "high" outcome increases.
The agent's utility function is some function of his wage minus his effort cost:
The principal wants to maximise his expected profit by choosing a state-dependent contract which induces the effort level that maximises the following profit function:
Model analysis
Here we assume that the agent is risk-averse. If the agent is risk-neutral, it does not matter whether effort is observable or not, and nobody is any worse off.
Observable effort
The agent has both a participation and an incentive constraint. The participation constraint ensures that the agent's reservation utility must be lower than his wage when he exerts either high or low effort, i.e. it is better to work than not at all. The incentive constraint is that , i.e. it's better to exert high effort than low effort.
When effort is observable, the incentive constraint is irrelevant. The principal can simply make wage conditional on effort, and will set
that is, the wage conditional on effort level just equals the agent's reservation utility plus the effort incurred. The principal can additionally set the wage conditional on its undesired effort to equal zero.
The principal prefers to induce high effort if and only if the expected payoff from inducing high effort is greater:
or equivalently,
where is the wage paid to the agent if he exerts a particular effort level.
Unobservable effort
When effort is unobservable, the principal can no longer make wage conditional on effort. The principal must make wage conditional on outcome instead, paying when the outcome is low and when the outcome is high.
These wages and must ensure that both the PC and IC are satisfied.
Under unobservable effort, the participation constraint can be written as follows, for either high or low effort:
Inducing low effort when effort is unobservable
If the principal wants to induce low effort, there is no change from the unobservable case. The principal can pay a fixed wage such that the participation constraint for low effort is satisfied with equality:
This simplifies to
which is exactly the PC in the case with observable effort. Note that because , if the PC for low effort is satisfied with equality, the PC for high effort will never be satisfied. So the principal is guaranteed to get low effort.
Inducing high effort when effort is unobservable
When effort is unobservable the principal must set wages such that the IC is satisfied. The incentive constraint can be written as follows:
That is to say, the agent will prefer to exert high effort to low effort when the expected utility from high effort exceeds the expected utility from low effort. This means that the difference between the low wage and the high wage must be high. To induce high effort, the principal must offer a low wage that is low enough to satisfy the IC. We rearrange the incentive constraint and take the inverse to obtain
As usual, it must also offer a wage high enough to satisfy the participation constraint:
in other words, that the certainty equivalent of the wage when exerting high effort must give the agent at least its reservation utility.
Effects of unobservable effort on welfare
The agent can never be worse off (or indeed, better off) because the principal always gives him a contract or a fixed wage that gives him utility exactly equal to his reservation utility.
If the principal wants to induce L effort in both states, then nobody is worse off. As I have shown, the principal can give exactly the wage needed to satisfy the lower participation constraint in both cases.
If the principal wants to induce H effort in both states, then the principal is worse off because of agency cost. Under observable effort the principal needs to pay a wage that exactly satisfies the participation constraint . Under unobservable effort it must also satisfy the participation constraint In both cases the certainty equivalent of the wage contract gives the agent a reservation utility . But because the agent is risk-averse, the expected income of the lottery must exceed the certainty equivalent. This is why the principal is worse off: it must pay a low wage low enough to incentivise high effort, but it must raise wages to compensate the agent's risk aversion as a result.
If the principal wants to induce H in the observable case but L in the unobservable one then it must be the case that the agency cost is greater than the increased expected surplus from inducing high effort. That must mean the principal is worse off.
Finally, it cannot be the case that the principal wants to induce L effort in the observable case but H effort in the unobservable case, because of a result akin to WARP: inducing H effort in the unobservable case gives strictly less payoff than inducing H effort in the observable case, so if the principal already prefers L in the observable case he will certainly prefer L in the unobservable case.
Signaling
Spencerian (1973) signaling game. Unlike screening, here it's the
Basic setup
The setup of the game is as follows:
- Nature assigns each worker either High () with probability or Low () type with probability .
- Each worker chooses education level increasing in education. The cost of education is , so High-types find it less costly.
- Each company thus specifies a wage schedule: some function mapping education to wage.
- Each worker's payoff is and each company's payoff is .
The key is to find all the Perfect Bayesian Equilibria (PBE) of the game and show that some are ruled out by the Intuitive Criterion. Recall in the PBE we must specify beliefs that are consistent with the strategies actually taken.
Pooling equilibrium
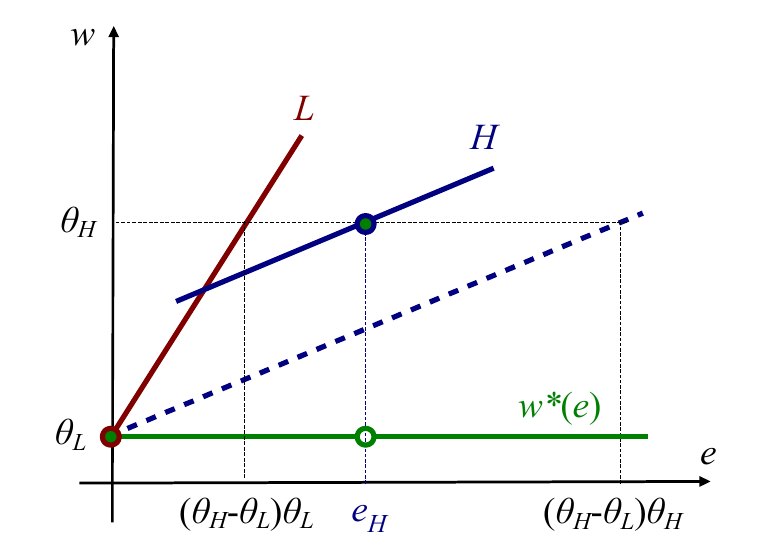
Let's first look at a pooling equilibrium. In a pooling equilibrium, both types set a common effort level , and the company pays wages equal to the expected productivity of the two types of workers.
In this equilibrium, the firm's belief that
and
Its wage schedule must therefore be something along the lines of:
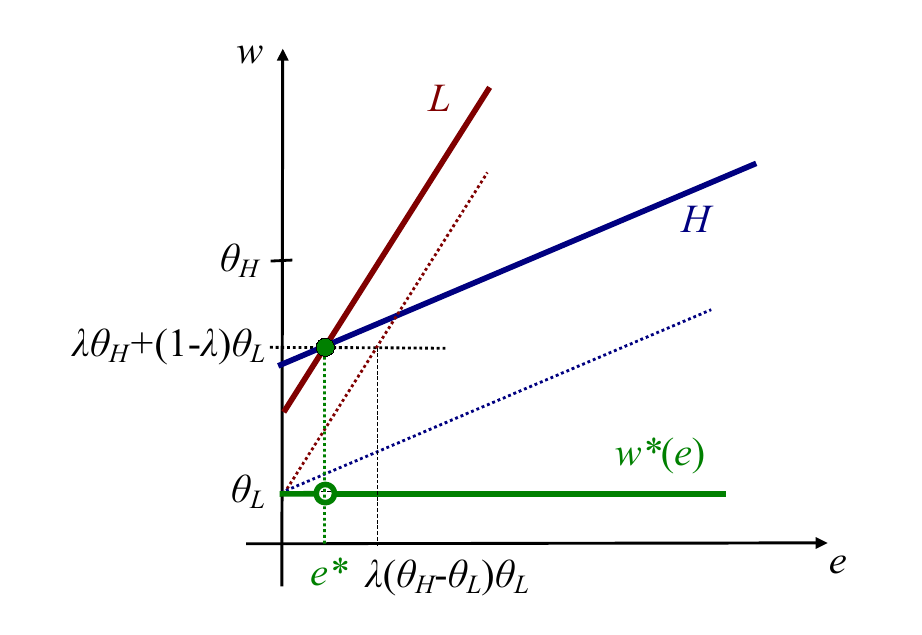
We can represent this in a diagram with wage on the y-axis and effort on the x-axis. The green line represents the wage schedule that the firm pays, and the lines labeled L and H respectively are the indifference curves of low- and high- ability workers respectively. (We can draw them in the regular convex fashions WLOG). Note that in this diagram better indifference curves lie to the north-west of worse ones. We can see that the indifference curves for H-types are flatter than for L-types.
We can see that there is no profitable deviation for either type. Given that firms pay the same amount for any higher effort, higher effort is obviously not profitable. What about lower effort? The dotted indifference curves denote the indifference curve each type of worker would be on if they deviated and chose zero effort. At this pooling equilibrium, both types of workers would be worse off. But this depends on . We must thus check that it is better for low-productivity workers to exert this pooling level of effort. That is,
or, rearranging to make the subject of the formula,
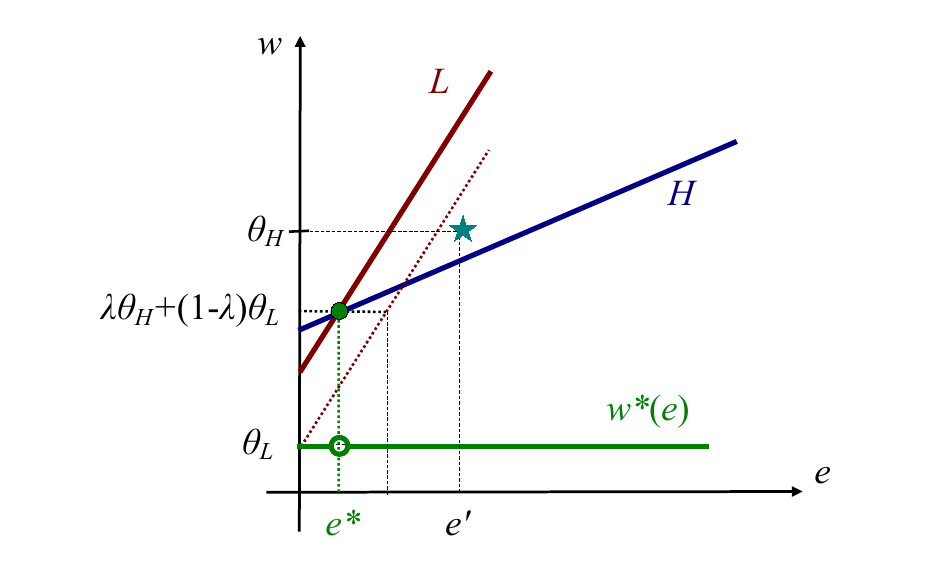
Separating equilibrium
In such an equilibrium, the firms have the belief
and
They thus pay
It must be the case that low-productivity workers find it less profitable to exert that high amount of effort. That is,
It must also be the case that high-productivity workers find it less profitable to exert no effort. That is,
Rearranging to make the subject of the formula, and combining the two equations, we obtain
It's worth noting that the the wage schedule the firm pays doesn't have to be exactly what I wrote. Here in Eso's slides the wage goes to even when , whereas in my treatment I have that the wage is above . It doesn't matter --- it's a bit like an "off-path" equilibrium.
The Intuitive Criterion rules out all pooling equilibria and non-minimally separating equilibria
The Intuitive Criterion says that if anyone deviates you should assume they are the type which could potentially gain from that deviation rather than the type that couldn't possibly gain.
Pooling equilibria cannot be possible in this game (It is possible with other payoff functions). Why? Suppose we are at the pooling equilibrium. Then there is some effort level, , where only a H-type has an incentive to deviate by exerting that level of effort and receiving a high wage. The diagram illustrates. A L-type would be worse off because that effort would be too costly. If that's the case, then the Intuitive Criterion tells us that , and so we have a profitable deviation.
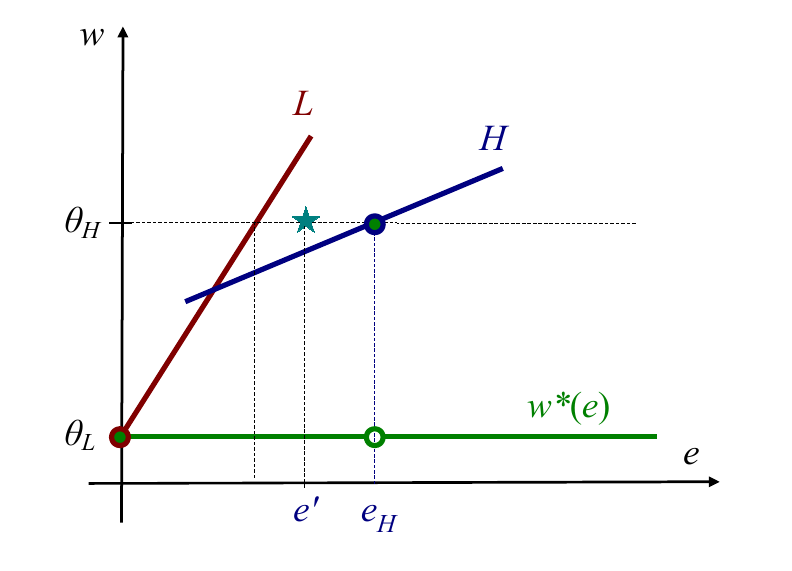
The Intuitive Criterion tells us that non-minimally separating equilibria cannot exist. A non-minimally separating equilibria is an equilibria where is higher than it "needs" to: that is, where the inequality condition for L-types preferring to exert no effort,
holds with strict inequality.
Consider the effort level such that the inequality condition binds with equality. Because it binds with equality, the Intuitive Criterion once again tells us that , and so we have a profitable deviation for H-types to exert less effort.
Mixed semi-separating equilibria
A competitive separating equilibrium may not exist!
The key in a competitive separating equilibrium is for firms to make zero profit. If the amount of effort is not continuous, but comes in discrete quantities, this may not be possible.
PYPs
9. "When prospective employees are able to signal their ability, competitive employers are no better off, employees with lower productivity are definitely worse off, and even employees with higher productivity might be worse off.” Do you agree? Does it follow that removing the ability to signal would result in a Pareto improvement?
- Competitive employers no better off: agree. Always 0 profit.
- Employees with lower productivity worse off: true without adverse selection, weakly false otherwise.
- Employees with higher productivity possibly worse off: if they were previously not signalling, now they have to signal, which can be costly. Whether or not they are worse off depends on the relative cost of the signal and the proportion of H- to L- types. If the proportion of H_types is high, and the cost of the signal is high, then the separating eqm can be worse-off for H types compared to the relatively high-paying pooling eqm.
- No it doesn't follow that removing signalling would be a PI because higher productivity employees can actually be better off. Evidently not a Pareto improvement if employees with higher productivity (can be) better off with signaling!
- Extension 1: adverse selection (if H-types have high reservation utility such that the pooling eqm of no effort cannot be sustained)
- Extension 2: non-costly signaling (if H-types have 0 or even negative signalling cost while L-types have some signaling cost)
Introduction
Basic model setup
Model analysis
Extensions: adverse selection and non-costly signaling.
9. There is a project with an uncertain outcome (high or low) that depends on the level of effort (high or low) exerted by whoever undertakes it – the high outcome is more likely when effort is high than when effort is low. If a social planner were making the decision, she would want high effort to be exerted. However, there is a risk-neutral principal that owns the project, and an agent who will undertake it on their behalf. If the agent is also risk neutral, explain what the principal would do and why. What level of effort will be exerted? From now on, assume that the agent is risk averse. When effort is observable, what level of effort will the principal specify, and how will they determine the wage? When effort is not observable, will the principal want to specify the same level of effort?
Basic model setup
There is a project with an uncertain outcome or depending on the agent's exerted effort. Here we assume that effort can only take low or high levels: that is, .
Let the probability of a "high" outcome conditional on the agent exerting effort level 1 be denoted as , mutatis mutandis for effort level 0. That is, and . Additionally, we demand that : if the agent exerts high effort, the probability of a "high" outcome increases.
The agent's utility function is some function of his wage minus his effort cost:
The social planner wishes to maximise social welfare. He thus chooses the level of effort such that social welfare is maximised. In this case, the level of effort that would be chosen is high. That means that
\begin{equation} (1-p(1))y^L + p(1)y^H -w(1) + f(w(1)) - e(1) > (1-p(0))y^L + p(0)y^H - w(0) + f(w(0)) - e(0), \end{equation}
or in other words that the total surplus (output less effort costs incurred) is greater when high effort is exerted compared to when low effort is exerted.
In contrast, the principal wants to maximise his expected profit by choosing a state-dependent contract which induces the effort level that maximises the following profit function:
The principal prefers to induce high effort if and only if the expected payoff from inducing high effort is greater:
or equivalently,
where is the wage paid to the agent if he exerts a particular effort level.
Note that this is exactly the same condition as the social planner's, because when the PC binds with equality, the principal pays a wage such that (plus some reservation wage). Therefore, , and the terms fall out.
2018 Q8. What is risk aversion? What do we mean when we say that Greg is more risk averse than Jamal? How might we test whether or not that assertion is true? What does “lottery A is more risky than lottery B” mean? How might we show this in theory, and in practice?
Risk aversion is the slope of the indifference curve in state-dependent space. It
Greg is more risk avers
2015 Q10. Pat argues, “Sure, I don’t like risk. But if I always choose the option with the higher expected value, over the long run the wins and losses will more or less cancel out, except that I will end up getting a higher payoff on average. So it is irrational to be averse to risk.” Evaluate Pat’s argument.
Basic model
Pat's argument goes along the following lines:
Suppose Pat starts off with $10 and has a utility function
He is offered a lottery of gaining $2 or losing $1 each with 50% probability. The expected value of this lottery is
But his certainty equivalent is
So he would not take the lottery.
But what if he is offered a series of lotteries? Over the long run, perhaps there are two lotteries in a row. Then his CE would be :
So it's a risk pooling argument: the probability of the median outcome is higher. And so in the long run it would make sense to accept the lottery if Pat is assured of similar future lotteries.
"It is irrational to be averse to risk": what does that actually mean? Recall that risk aversion really just means decreasing marginal utility of wealth. But there is a second definition, more "pedestrian": that is that a risk-averse person would not take a fair (or even somewhat positive EV) lottery. Pam's argument is that: even if you are risk-averse in definition (1), if you think of lotteries as a series of lotteries, you should not be risk averse according to definition (2).